
I have been mulling over compensated bridges for some time now, and I just had to figure them out or go crazy. So, I started researching the issue, and I finally came up with something of an explanation. Then, I thought, "Why not share this with the folks on web"?
So, here it is. If you have an intolerance for acoustical physics or for very long and detailed explanations, click on your "Back" button now or click here to go back to my Music Page. I find this stuff fascinating, but I am sure that it bores most people.
It began the first time I saw a Moon bridge on a banjo down at the Music Emporium. It puzzled me how a curved bridge could possibly play in tune given that the frets on the banjo go straight across the neck.
Every high school physics student knows that the frequency of vibration of a string is proportional to the length of the string, and therefore if you fret the string half way up its length (at the 12th fret) the frequency of the string will be doubled and therefore the string will play an octave higher than the unfretted string. Pretty simple.
But, if the bridge is curved, then some of the strings *must* be too long or too short to be fretted properly by the straight frets. It just does not make sense that a curved bridge, where all the strings are different lengths, can play in tune against the straight frets. The 12th fret will divide some of them in half, but not the others. In fact, it almost guarantees that the instrument can be set up to play in tune on only one of the strings...or at most a couple of them.
What gives? Here is a photo of what I am talking about:
You can see that the frets on the left go straight across the neck, whereas the Moon bridge on the right is curved. According to high school physics this arrangement cannot possibly work.
The Moon bridge is called a "compensated" bridge, and its shape actually makes the instrument play better in tune. The different string lengths provided by the bridge adjust the intonation of the different strings to make them fret properly. That is nice to know, but it does not really explain to me *why* the string lengths must be different. So I set off to see if I could discover a reason behind this strange effect.
Having had an interest in physics in the distant past, I went straight to my old physics books and started researching.
So here we go.... This is what I found out about why the frequency of a vibrating string in relation to its length is not as obvious and simple as they taught us in high school physics.
Oh! Before I start, I should mention that my source for this material is mostly "Fundamentals of Musical Acoustics" by Arthur H. Benade, 1976 edition. I also used that classic work by Hermann Helmholtz, "On The Sensations of Tone". I did not make this stuff up. The equations used here are not the result of work done by me. I got them from the books. Due credit has been given.
OK. Here we go. Hit your Back button now, or descend into the depths of acoustic physics.
A perfectly flexible string, which is stretched between two rigid supports will vibrate at a fundamental frequency plus a bunch of harmonic frequencies. The harmonic frequencies are integral multiples of the fundamental frequency. So, the fundamental tone is caused by the string vibrating at frequency n, and the first harmonic is the tone caused by a superimposed vibration of the string at frequency 2n. Similarly, the second harmonic is vibrating at frequency 3n. All of these tones are vibrating on the same string at the same time, and the magnitudes of their vibrations are additive.
The different harmonics vibrate at different amplitudes. Normally the amplitude of a harmonic decreases as the number of the harmonic increases, for example the loudness of the first harmonic is less than the loudness of the fundamental tone. The loudness of the second harmonic is generally less than that of the first two, etc. (This is not always the case, such as when you chime a string by damping out the fundamental tone). To illustrate what is going on, I have created some animated images. The image below shows a string that has been stretched in the middle, ready to pluck it, but not yet released.
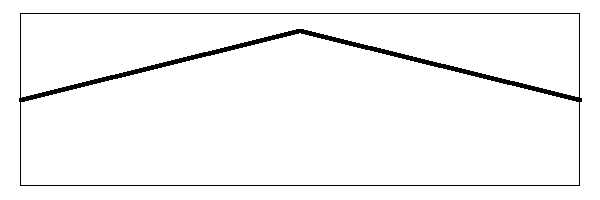
The string is the dark line inside of the box. The nut is at the end of the string on the left hand side, and the bridge is at the end of the string on the right hand side. To keep the images simple I have not drawn the nut and the bridge, but they are the assumed anchor points for the string. The distances that the string vibrates are exaggerated in the drawings to illustrate their movements better. I have also slowed down the frequencies of vibration so that you can see them.
After the stretched string is released, it will vibrate up and down as shown below.
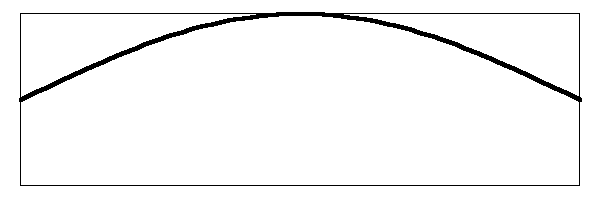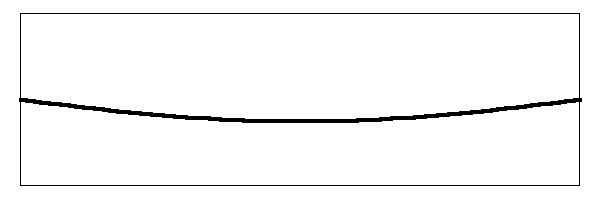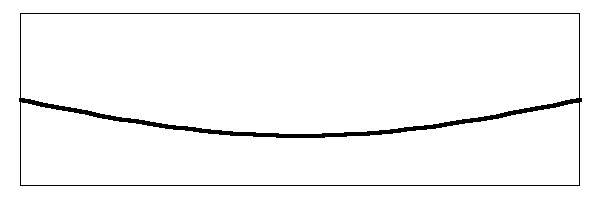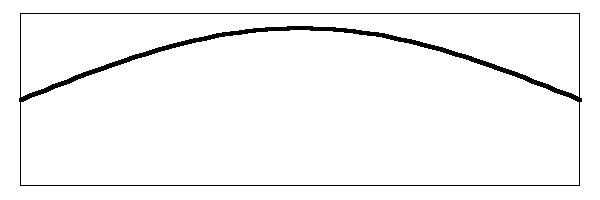
This is the fundamental note of the vibrating string. When a real string vibrates like this at an audible frequency some of the energy of the string is transferred through the bridge and into the head. The head moves the air and the sound is propagated to your ears. So far this is simple stuff. What complicates it is that other modes of vibration are set up simultaneously in the string. Below is an image of the string vibrating in the first harmonic.
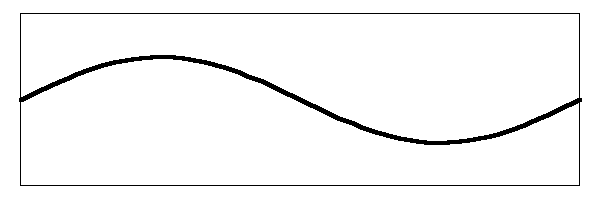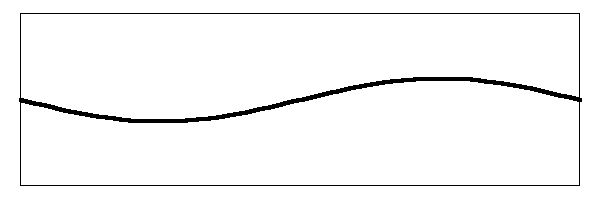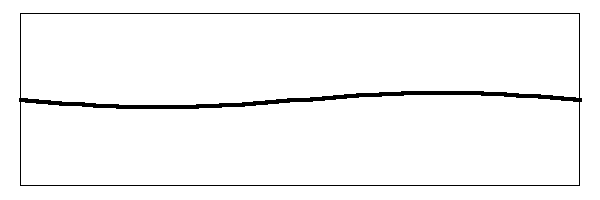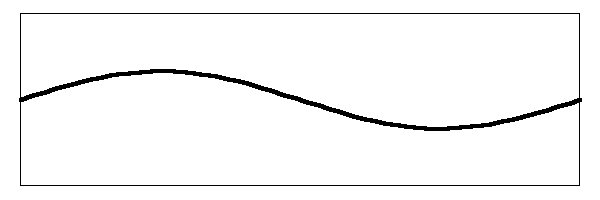
There are a couple of things to notice in the image. For example, the amplitude of the vibration (which is just the distance that the string moves) is less for this mode than it is for the fundamental mode. That is because the part of the string in this mode that is vibrating up and down was not stretched as far as it was for the fundamental. The largest deviation of stretch is in the center of the string, where the fundamental frequency is vibrating. However, in this mode the center of the string is not moving. That is called a "node". The part of the string that is moving (which is about a third of the way up from the nut or the bridge) is not stretched as far so it does not vibrate as far.
You may also notice that the string is vibrating twice as fast as it does for the fundamental frequency. When you hear this note, you will hear a tone that is one octave above the tone for the fundamental frequency.
What actually happens on the string is that both of the modes of vibration are occurring at the same time. By the physical law of "superposition", the two vibrations are simply added. What is really happening on the string is that it is vibrating like this:
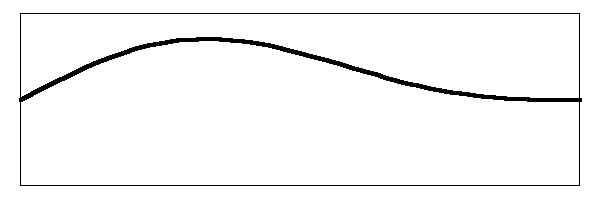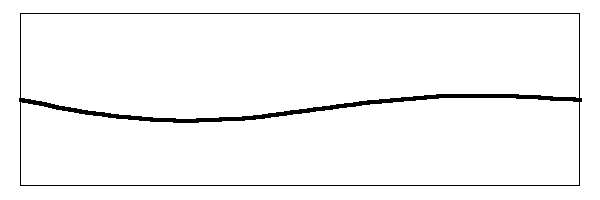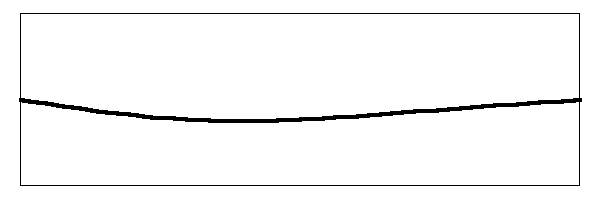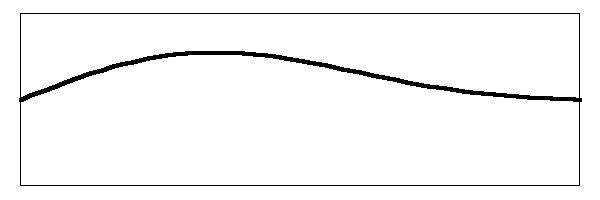
It is difficult to see both of those vibrational modes in the way the string jiggles around, but that is what is causing it. In the image I have simply added the two vibrations together.
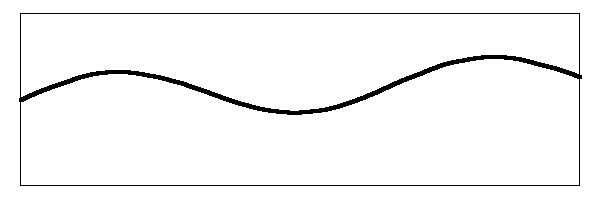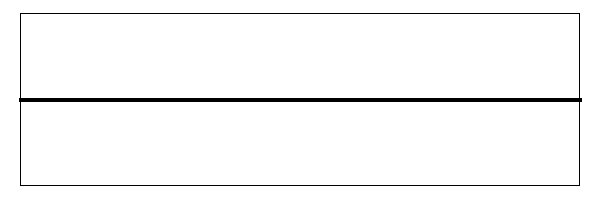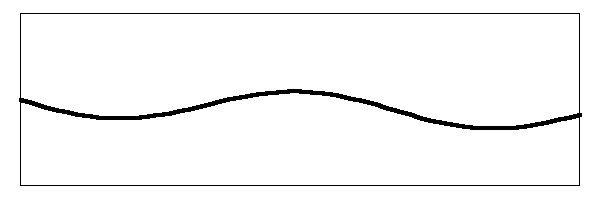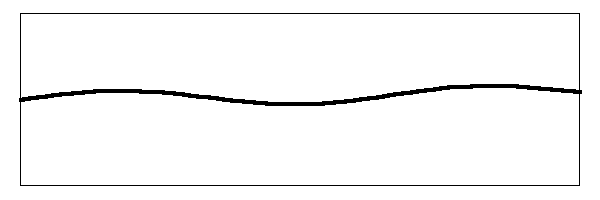
But there is more to it than that. There are other harmonic modes of vibration. If we look at the next harmonic, the second harmonic, we would see the string moving like this:
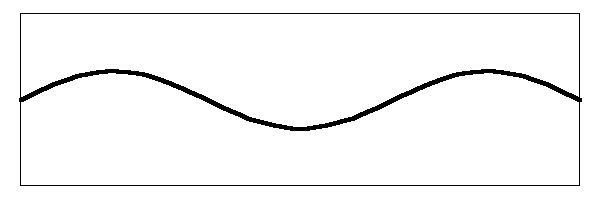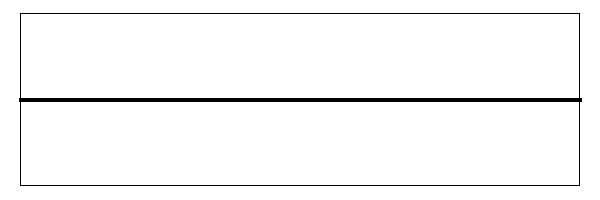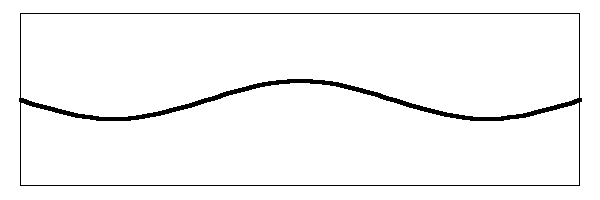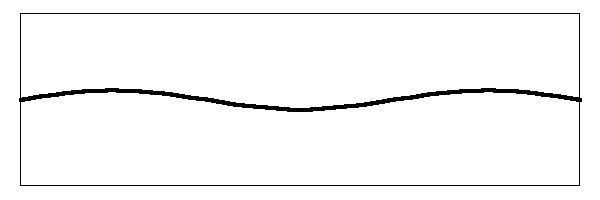
Notice that there are now three places on the string that are moving up and down. There are two nodes where the string does not move. The string is vibrating at three times the frequency of the fundamental. The amplitude of the vibration is smaller than the amplitude of both the fundamental and the amplitude of the first harmonic.
Just like the fundamental mode and the first harmonic mode, the second harmonic mode also vibrates the string simultaneously along with the other two. What is really happening on the string looks something like this:
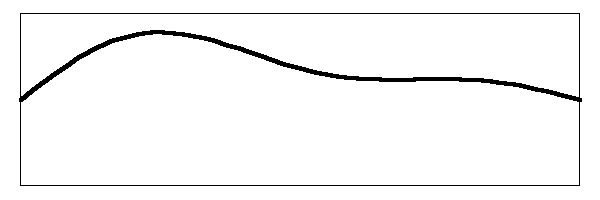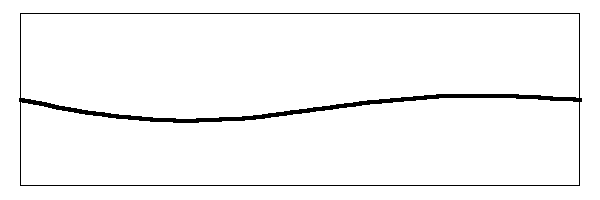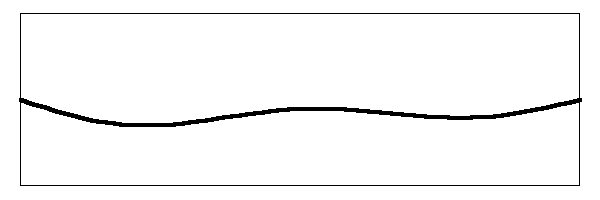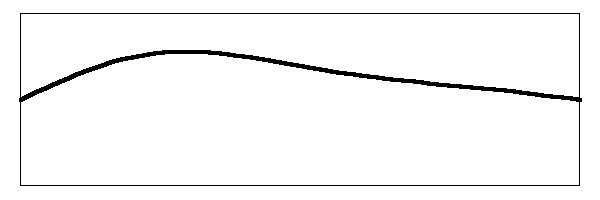
Wow! That thing is flopping around like a wet noodle.
It does not end there. There are theoretically an infinite number of these vibrational modes, although in a real string their amplitudes decrease rapidly until the higher modes are not real contributors to the sound. For simplicity I am showing only the first three modes of vibration.
But there is still more to show. The basic sound of the string depends on how many harmonics are mixed and what their relative amplitudes are. You see, the relative amplitudes of the partials are not fixed at the levels I showed in the above images. Where you pluck the string determines which of the harmonics will dominate the sound. If you pluck the string in the middle, the fundamental tone will dominate. But what happens if you pluck the string closer to the bridge?
If you stretch the string from a location that is closer to the bridge, your starting point (before you release the string) will look like this:
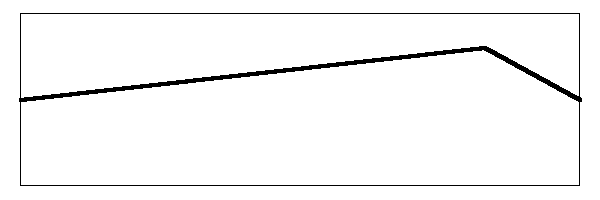
You can see that the largest deviation of the string is no longer over the center where the fundamental mode vibrates. It is actually larger over the parts of the string where the first and second harmonics move. when you release the string it will impart a larger amplitude in the mode that has that part of the string moving up and down. Here is a drawing of the string vibrating at the first harmonic with a larger amplitude.
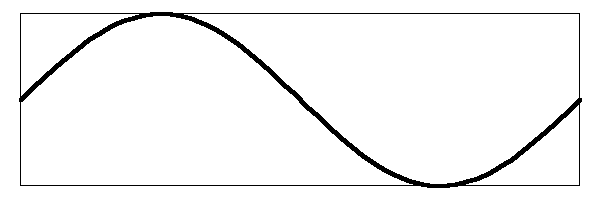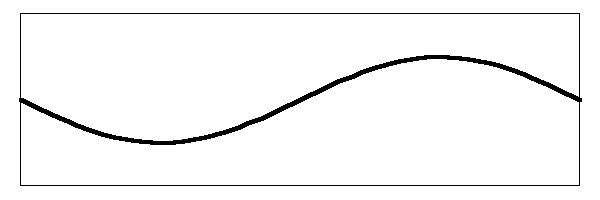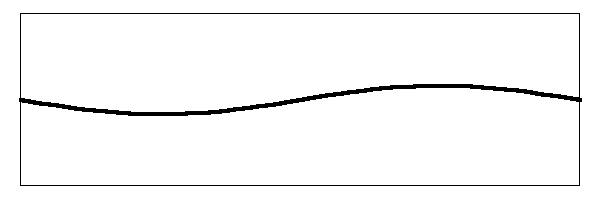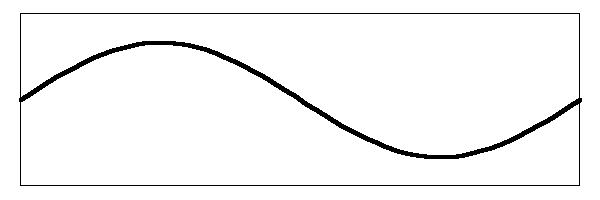
In this situation, the fundamental mode, where the center of the string is moving up and down, will have less amplitude since the pluck point is off center. This will also be true of the second harmonic. When you add all the frequencies together, you will get a string that is vibrating like the image below:
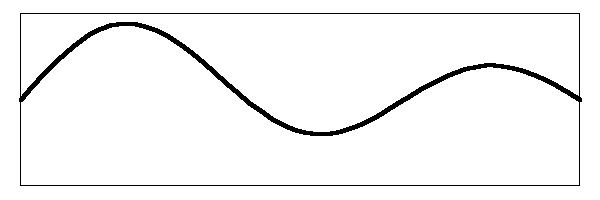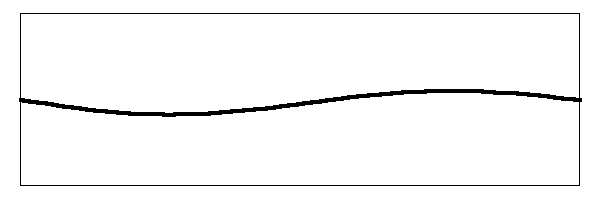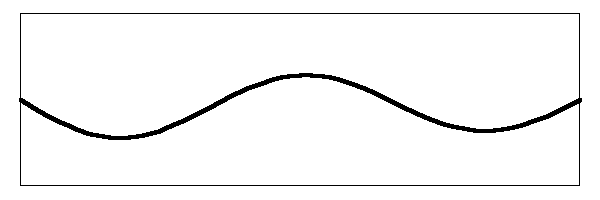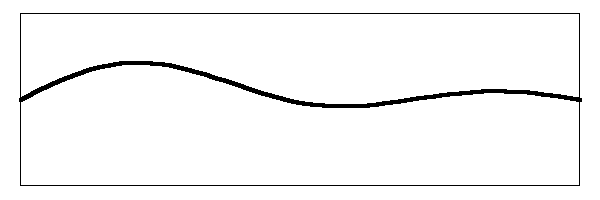
This is quite a different sort of action from when the string was plucked in the middle. Compare to the previous image here and then click on your browser's Back button to get back to here. This string contains the same harmonic frequencies as the previous one, but mixed with different amplitudes. This one looks positively frenetic compared to the one where it is plucked in the middle of the string. In fact, this one will have the characteristic "twangy" sound of the banjo. That is why the banjo sounds more twangy and less mellow when you pluck it near the bridge.
OK. You are probably getting dizzy from viewing all of those animations, so lets move on.
Now that the vibrational modes of the string are understood, we can continue on to the effect of fretting the string on the finger board. If you fret the string in the middle, the length of the string is cut in half, and the frequency of the string vibration will double. This gives you an octave tone. Fretting at other proportional positions will give proportional frequencies.
If these facts are not already known to you, there are numerous web sites and books that will explain it. It is the basic physics of vibrating strings that we are taught in high school. This is the theory that tells me that straight frets require a straight bridge in order to play in tune. If the bridge is curved, then the straight fret on the finger board cannot be at the half way mark between the nut and the fret on two strings that have different lengths.
However, I have discovered that there is a little more to the acoustic physics than is described in the simplified explanation.
When you fret the string, you must push the string down to the fret. This stretches the previously straight string and makes a V out of it. Since the sides of the V are, added together, longer than the straight string, you have made the string a bit longer and therefore stretched it. This increases the tension on the string, raising its frequency. The frequency of the string vibration depends on the tension of the string as well as its length, which is why we can tune the string by stretching it. So, a string which has been stretched a bit by fretting will play just a little bit sharp, and to compensate for that you must move the bridge a little bit farther away from the nut to make it play in tune.
That still does not explain the curved bridge because all of the strings stretch when they are fretted. So all of the strings should go sharp by the same amount and all you need to do is move the straight bridge back toward the tailpiece.
But wait! Keep reading. It turns out that the stretching of the string affects the tone differently on the different size strings.
In fact, here is the formula* (from Dr. Benade's book) for all the frequencies of the stretched string. The formula includes the tension of the string as well as its length:
| fn = |
|
|
|
where
To calculate the fundamental frequency, set n = 1 and run the formula. To calculate the second harmonic, set n = 2 and run the formula. The second harmonic, as can be seen from the formula, is n times the fundamental.
So what? Well, there are some relevant bits of information which can be extracted from the formula. For example, the frequency of the fundamental (where n = 1) is proportional to the square root of the tension. So, to double the frequency you must quadruple the tension..... square root of four is two. Interesting? To make the string sharper requires a lot of added tension. Be careful tuning up or you will snap that string!
Also, the frequency is *inversely* proportional to the radius of the string. That makes sense. A fatter string will oscillate more slowly, so the frequency goes down. If all the strings are the same length, a fatter string, such as the G string will fret a bit flatter than the rest since it is a bit thicker than the rest and they are all being stretched the same amount. So one would think that the thicker string would require a shorter length to bring it back up to pitch when fretted, which implies that the bridge should be compensated toward the nut, not toward the tailpiece........a result which is not borne out by our experience with compensation.
But it isn't quite that simple. There's more.
The string is not really a perfectly flexible string. It has rigidity (stiffness). You can feel the rigidity if you take a string in your hands and bend it into a tight arc. There is resistance there, and that is the rigidity. The thicker the string, the more rigid it is. You can feel the difference in the rigidity between the small D string and the larger G string.
Mathematically you can look at the string as being a rigid bar attached at both ends, at the nut and at the bridge. Of course, it is not a *very* rigid bar, but it has some rigidity nonetheless.
The formula for a rigid bar fastened by hinges at both ends is different from the formula for a flexible string under tension. It is:
| fn = |
|
|
|
where
The modulus of elasticity is just the amount that the bar is deformed for a specific force, or stress. There is no tension, T, in the formula because the bar is not stretched.
Anyway, looking at the new formula we can see that there are some interesting differences between this formula and the formula for the stretched string. For example, the harmonic frequencies are no longer integral multiples of the fundamental frequency. In fact, they increase as the square of the harmonic number times the fundamental, as evidenced by the n2 factor in the formula. So, the first harmonic of the rigid bar is 4 times the fundamental, and the second harmonic is 9 times the fundamental, etc. This changes the sound coming from the string by enhancing some of the higher harmonics, but not all of them.
Another difference is that the radius of the bar is now in the numerator rather than in the denominator. So, as the radius of the bar is made larger, the frequency goes *up* rather than down. That's interesting. A fatter string now has a higher pitch than a thinner string under circumstances where the other factors are the same.
Also, the length of the bar, L, is squared. So, if the length of the bar is doubled, the frequency goes down 4 times, or, two octaves. For the stretched string, the frequency goes down one octave if you double its length.
Confused yet?
There's more.
Since the string on your banjo has characteristics of both an ideal string under tension *and* an ideal rigid bar hinged at both ends, the two formulae above must be mixed to obtain the actual effect of the string length on the frequency of vibration.
That mixing formula (right out of the book) is:
| fn = |
|
where
fn(flexible) is the calculated frequency of the flexible string for harmonic n
and
fn(bar) is the calculated frequency of the string as a rigid bar for harmonic n
or, to put the formula into words, it is the square root of the first formula squared plus the second formula squared. Sort of like a Pythagorean theorem for string frequencies.
Calculate the frequency of the stretched string and square it; then calculate the frequency of the rigid bar and square it; then add them together and take the square root.
If we assume that the contribution to the frequency made by the stiffness of the string is small, this can be resolved to the following, simplified equation:
| fn = n f1(flexible) (1 + Jn2) |
which just says that the frequency is the flexible string fundamental frequency (mode 1) times the harmonic number plus the same flexible string fundamental frequency times a small correction for the stiffness of the string, J. The correction for the stiffness is J n2, where J is:
| J | = |
|
So, now look at that radius effect, r (which is determined by the gauge of the string) in the formula used to calculate J. It is now raised to the 4th power! And the frequency goes up as r goes up! This is due to the stiffness in the string as opposed to the normally assumed ideally flexible string. If you double r you raise its effect by 16 times!
When stretching a string to fret it, the effect of the thickness of the ideal stretched string on the frequency change is to make it go *flat* (from the flexible calculations), but it will also make it go *sharp* proportional to the fourth power of the thickness of the string (from the rigid bar calculations).
Added up, the effect is that the thicker and more rigid the string, the sharper it will go when fretted.
To quote Dr. Benade's book:
"... the inharmonicity is reduced if one uses the longest, tautest, and slenderest string that meets all the other requirements which may be laid down upon a musical string."
So you see, there is some pretty complex stuff actually going on when you pluck your banjo string.
But wait!
That's not all!
The stiff string is not really connected to perfectly rigid supports on both ends. In fact, if it were, you would not be able to hear anything at all. The vibrating string must impart some of its energy to the banjo head or no sound will come out. The truth is that one end, the bridge end, is connected to a fairly flexible support,...the head of the banjo.
How does that effect the length of the vibrating string?
Well, when you connect the vibrating string to a flexible support, it turns out that you can treat the string as an oscillator which is driving a mass on a spring (the head). That just means that the banjo head has its own mass and fundamental frequency, and it interacts, through the bridge, with the vibrating string. Here is a drawing which illustrates the situation.
This actually changes the effective length of the string. In the figure, Fs stands for the frequency of the string and Fh stands for the frequency of the head. The arrows and dotted lines indicate the effective string length in each case.
To illustrate what is going on here, I return to my animations of the string dynamics. Below is the string animated to show the situation where the string is anchored at the nut, but the bridge is being allowed to move up and down to drive the head. The figure shows only the fundamental vibrating mode.
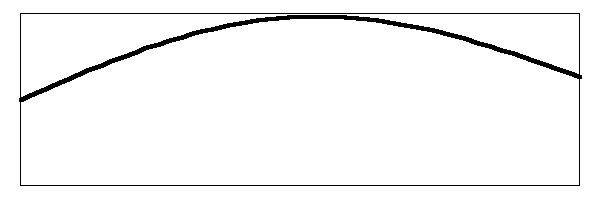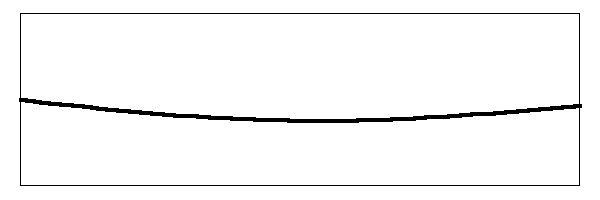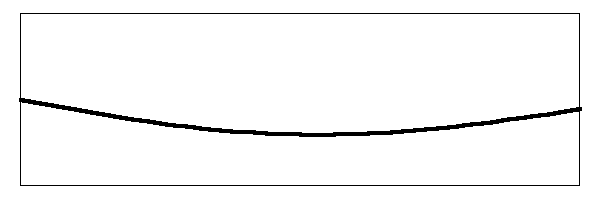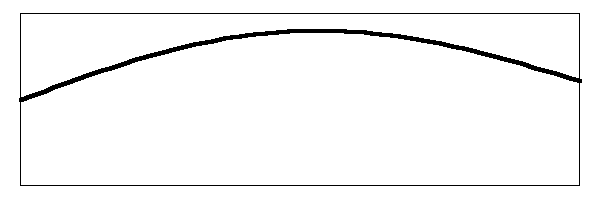
The nut is on the left hand side and does not move. The bridge is on the right and side and moves up and down driving the head as you can see in the animation. A similar effect occurs in the other modes, such as the first harmonic:
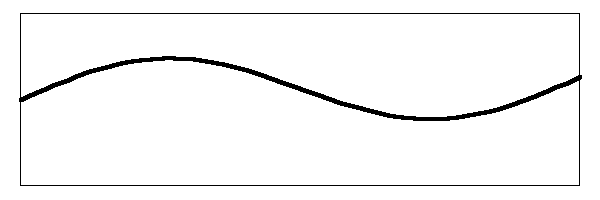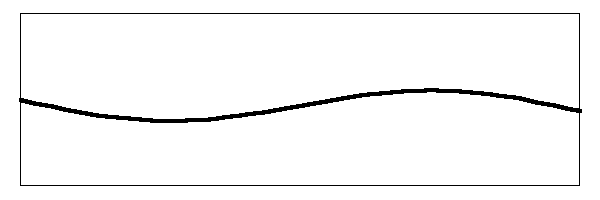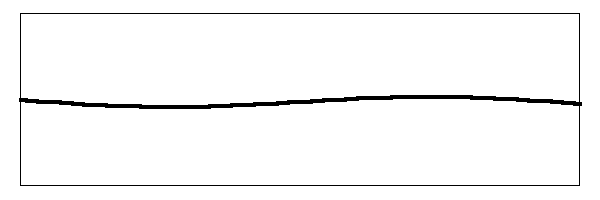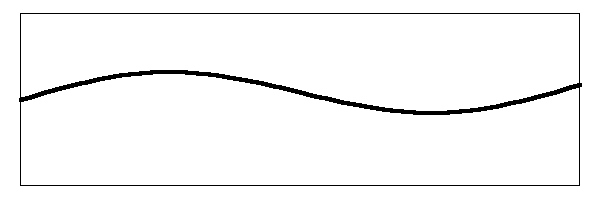
Below is the second harmonic with a moving bridge.
When you add them all up, the string moves something like this:
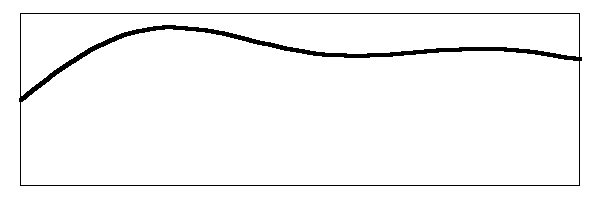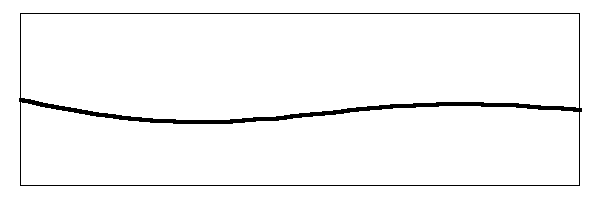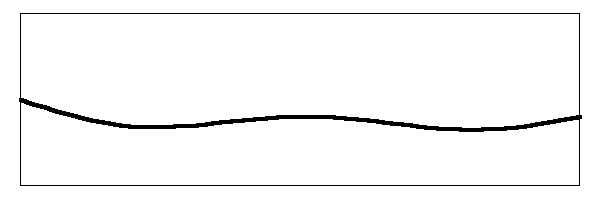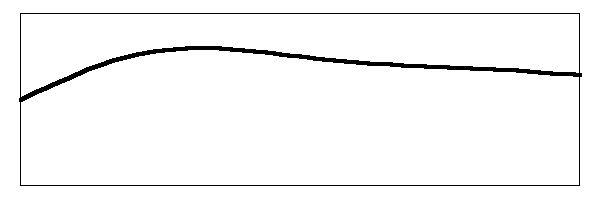
There's our jiggling noodle of a string going even more nuts than before. Watch the action of the bridge on the right hand side of the drawing and you can see the complex movement that is going on. That is what you hear when you pluck the banjo. The image above assumes that you have plucked the string in the middle. If you pluck the string closer to the bridge, you get an enhancement of the amplitude of the higher harmonics so the string movement will look more like this:
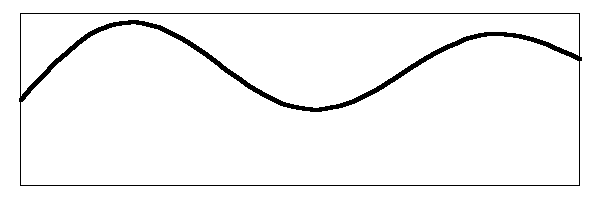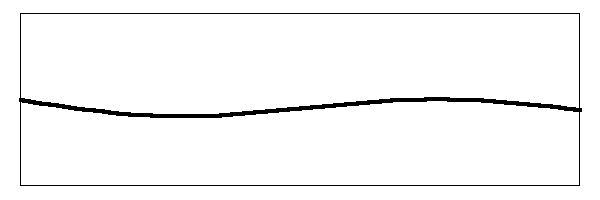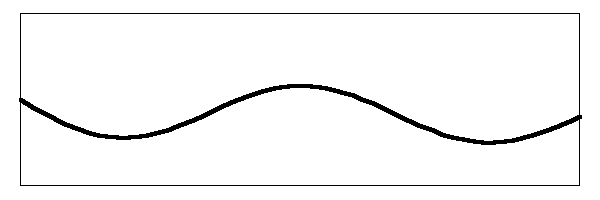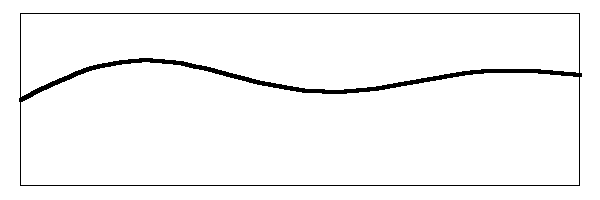
The head is truly jangling around now. But that still is not the end of the story. The fact that the head itself has a resonant frequency changes the effective length of the string because of the interaction between the two oscillators (the string and the head). I do not have the time or the skills to derive the following conclusions, but I will trust that Dr. Benade did a good job of it. Here are his conclusions.
To make a long story short, (too late!)..... if the fundamental frequency of the string (Fs) is lower than the fundamental frequency of the head (Fh), the length of the string is made effectively longer, and its vibrating frequency is made effectively lower. The string vibrates too slowly to make the head resonate, so it just throws it around in phase with the string. So the head just follows the movements of the end of the string and acts as a weight, slowing it down. Slowing down the vibrations of the string have a similar effect to having a longer string. So the effective length of the string is longer than its real length.
In a similar way, if the fundamental of the string is higher than the fundamental of the head, the length of the string is effectively shorter, and the pitch is raised. The head is trying to keep up, but it gets behind because it is too slow in relation to the speed of the string, so it vibrates out of phase with the string. The string is wiggling all over the place, while the head is just sort of sitting there, unable to move much. In fact it vibrates counter to the string, and moves the node of vibration up along the string toward the nut. The string is effectively shorter than its real length.
So, the bottom line is that, depending upon how tight the head tension is (which effects the fundamental frequency of the head) and how heavy the head is (likewise) and the weight of the bridge (which is part of the head/bridge oscillator system) and the height of the bridge (which acts as a lever arm to transfer the string vibration to the head more efficiently) and the relationship of the fundamental frequency of each string to the fundamental frequency of the head..........(breathe!) the strings are either longer or shorter in their effective length than they are in their real length, which effects their pitch when fretted.
Whew!
But wait! We're not done yet.
Our model of the head being a simple mass on a spring over-simplifies the real situation. The vibrating head is a complex resonator like the string. It has much more going on than a simple fundamental frequency. As well as having harmonic frequencies, it also has vibrating modes in which the head vibrates in different locations across the surface of the head. In fact, the head is a much more complex vibrating system than the string. You can see animated images of the vibration modes of a circular membrane at the wikipedia or simply search the net for "drum vibration modes". Here are some very simplified examples of what is going on.
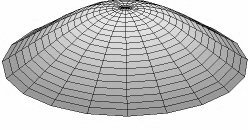
Mode 1**, the fundamental mode, is where the head simply moves up and down all together. Here is an image (borrowed from the Wikipedia). The moving part is the center of the head. Just imagine that you are pushing on the center of the head with your finger to push it away from the resonator and then pushing it back toward the resonator. The whole head just flies back and forth in one piece.
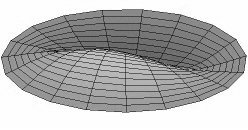
Mode 2** is more complex. Different sides of the head move in and out with opposite timing. Imagine that you are pushing the head down near the tail piece, and simultaneously (with another finger) pushing it up near the neck. Then, you reverse your fingers and do it the other way. So you have two bumps going up and down in opposite directions on opposite sides of the banjo. It can also vibrate in Mode 2 with the vibrating parts at the sides of the head instead of at the neck and tailpiece. In fact, the nodes could be anywhere around the circumference of the head.
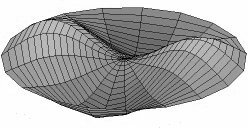
Mode 3**. Opposite sides of the head move in a similar manner to mode 2, but in the same direction at the same time, while the sides at 90 degrees go in the opposite direction. You need four fingers to do this one. Fingers at neck and heel push out, while fingers at top and bottom push in. Then reverse direction. Four bumps going in and out at once, two and two.
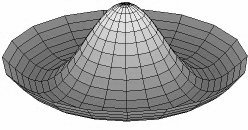
Mode 4**. The center part of the banjo head goes up and down, but the outside ring, near the tone ring goes in the opposite direction. You have a mountain and a moat going back and forth.
All of these modes (and more) are going on at the same time as the head vibrates. There are many more modes, and you should go out to the wikipedia to see them.
The frequency ratios of the different string vibrational modes are integral..... the frequency of mode 2 (the second harmonic) of the string is 2 times the frequency of mode 1 (the fundamental). Pretty simple.
However......... The frequency ratios of the head's modes are not so simple. Here is a table of them:
| Mode | Multiplier |
| 1 | 1.000 |
| 2 | 1.593 |
| 3 | 2.135 |
| 4 | 2.295 |
But wait!
The head also has stiffness as well as flexibility. And the relation of the perfectly flexible head under tension to its cousin, the rigid plate hinged at the edges is very similar to the relationship between the perfectly flexible string and its cousin the rigid bar.
The frequency ratios of the modes of the rigid plate are:
| mode | multiplier |
| 1 | 1.000 |
| 2 | 2.092 |
| 3 | 3.427 |
| 4 | 3.910 |
I have no idea what the formula is for mixing these two together. My head is starting to hurt.
So, you see there is a lot of stuff going on with the vibration of the banjo head too. So, what, then, is the frequency of the flexible/stiff head in relation to the frequency of the flexible/stiff string which is making it vibrate which effects the effective string length? I suppose it depends on where the bridge sits on the head. Or where that part of the bridge on which a particular string is resting is sitting on the head.
But wait!
(really.... I'm almost done.....don't hang up)
The fret board is not set up to play notes in the "natural" intonation. A normal fretboard is keyed to the equal tempered scale. I do not want to go into the details of tempering scales and wolf tones and all of that, but let it suffice to say that the equal tempered scale detunes the intervals very slightly so that it is possible to play the instrument in more than one key. If the scale were not equal tempered, you would have to retune the banjo to play in a different key. It takes the differences in tuning between the keys and sort of spreads the errors around so that you don't notice them as much.
What does that have to do with the compensated bridge? Well, just that the tuning of the strings is a compromise anyway. They will always be out of tune in a subtle way depending on what key you are playing in. So, the bridge must be set to a compromise position in order to make the equal temperament work well enough to sound good playing in all the normal keys.
OK. That's it. I am out of steam.
I won't address heat and humidity and the pot slightly out of round and tone rings and the resonance of the air in the resonator (or the air between your gut and the head for you openback frailers) or the modal resonances of the neck and the particular wood that is used to make the neck or the modal resonances of the room in which you are playing which may sound trivial but it is not, which will be obvious to you if you have ever played your banjo in the bathroom....... (don't ask).
What is the point of all this? !! Why in the world would anyone *care* to even go through all of this? !!
I just wanted to understand the complexity of what is happening when I play the strings on the banjo. Don't memorize any of this stuff. The compensated bridge takes into account all of these factors by adjusting the lengths of the strings to make them play in tune down the neck. Trial and error. Cut to fit. You can't even measure most of what is going on.
There are so many variables which interact in complex ways that it is impossible to calculate how the strings must be set to make them play in tune. So we do the best we can and try stuff until it works. Some of my banjos play just fine with a straight bridge which is canted to compensate it. Others use a bridge that compensates mostly the middle string. My mountain banjo has a home-made circular bridge on it which compensates the center string by about 3/8 of an inch. You just have to try stuff until you find what works..... mess around... cut to fit. When it sounds right it *is* right.
Or play fretless.
I figure the moon bridge this way:
The first string notch on the bridge is set for the smallest string, the D string. Then, as the diameter of the strings go up, they play a little bit sharper when they are fretted because of the effect of their stiffness, so the bridge must bow out toward the tailpiece to correct for that. This works through the third string, which is the last straight steel string. The fourth string is wound around a very thin core, and it is in reality thinner than the third string. So it has very little stiffness compared to the G string, and it plays a bit flatter again. So the bridge moves a bit toward the nut again. Finally, the 5th string is the same size as the first string, so the bridge moves up to where it started.
So there you have it. The curved bridge plays in tune with the straight frets.
Whew! I'm done.
Aren't you glad you asked? What? You didn't ask?
Oops. Never mind.
Brian
(The Devil made me do it)
Back to the Music Page.
*All of these equations can be found in Fundamentals of Musical Acoustics by Arthur H. Benade, Oxford University Press, London, 1976, Library of Congress Catalogue card number 75-2546 Section 16.5 "Vibration Physics of Real Strings", page 313.
**Image borrowed from the wikipedia .
Initial upload date February 16, 2009